Easy-to-use comfortable interface
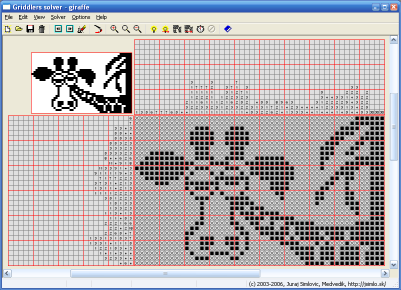
Compact interface uses most of the window space for the main puzzle. The grid is usually large enough for solving even on smaller displays. Each opened puzzle is automatically fitted and centered to the actual window size, but can also be zoomed in or out, resized or scrolled.
Besides the grid, the main window includes only a small toolbar and a statusbar, providing as much space for the puzzle as possible. The entire solving and navigation can be done by mouse and all instruments are placed in a way to simplify and ease the puzzling.
To access menu items quickly, nearly each menu item has its keyboard shortcut (hotkey).
Powerful and quick auto-solver
Upon difficulties with solving, there is always a ready-to-use auto-solver, which works the same way as humans do. Its hints are always logical steps in the solution. It never gives a hint that can not be discovered at the current state of the solving process. This is very useful, when you have no idea where to continue. The auto-solver will help you find the spot.
While the auto-solver works in steps, you may also let it run in a loop and watch the entire solving process in a quick movie.
The andvanced auto-solver is able to solve all griddlers included in the package. However, it should be able to solve any griddler that is also solvable by a human. This entire project was started mainly to implement an all-solving machine, and it was quite sucessful. By now, there is only one submitted griddler that takes more time to finish, than it is fair.
Note: If you ever find a griddler, that my solver could not solve, please submit it and include its picture as well. I would like to challenge it myself. And possibly improve my solver as well.
Simple editor
The application also includes an editor. To start editing, you only need to switch to the editor mode and everything else is the same. By clicking on clues with mouse buttons you raise or decrease them. Or you may choose to re-generate all the clues from the current picture.
Many puzzles from other users
Large and growing repository of personally selected griddlers is included in the download package for you to start solving or watching the auto-solver. All puzzles were created and submitted by the end users. All of them were checked for solvability and uniqueness of solution. They are categorized according to their difficulty level. All of them can be solved with the included auto-solver.
Easy-to-edit savefiles
If you would prefer to edit griddlers by a text editor, you may do so. The savefile format is very easy. No binary data, only plain text is used. Furthermore, there is only one file format for solved griddlers, for partialy solved griddlers and even for cleared puzzles, ready for puzzling. Actually, all griddlres packed within the download package are saved with picture. There is no reason to deliver them cleared, because all of them could be completely auto-solved within seconds or minutes anyway.
One may suggest that by delivering solved puzzles all the fun is diminished. Well, if you think so, you may use an option to Auto-clear the picture upon loading, which clears each picture when a griddler is loaded before displaying it. See? No fun got lost.. :)
About Griddlers?
Griddlers are logic puzzles, in which cells in a puzzle grid have to be coloured according to numbers given at the sides of the grid. The puzzle then reveals a hidden picture.
The numbers, also called clues, measure how many unbroken lines of filled-in squares there are in any given row or column. For example, a clue of "4 8 3" would mean that there are sets of four, eight, and three filled squares, in that order, with at least one blank square between each successive groups.
How to solve?
To solve a griddler puzzle, you have to come to logic conclusions, step by step, which squares are to be coloured and which should remain blank. Determining which squares will definitely remain blank is just as important as determining which squares will be coloured in, which is why you need to mark blank squares as well as fill the coloured ones. It is very important to use deterministic logic only and never to guess, because even a small single mistake can propagate very quickly far away and ruin the entire solution later.
That's it?
Some difficult puzzles may also require "what if?" reasoning with contradictions and other more advanced techniques. Learning to solve griddlers puzzles is fun, because you can already solve a few nice pictures by applying just simple logic. The real puzzling joy comes, when you start hard puzzles, though.
Mistakes!
A mistake usually comes to the surface only after a while, when it is already very difficult to trace it and correct the puzzle. Only te most advanced solvers are usually able to fix and finish a ruined puzzle, because even a small mistake can spread very far. The picture may help to find it, but starting over is usually much more efficient.
